Encryption
Introduction
• Cryptography is a method of storing and transmitting data in a form that only those it is intended for can read and process. It is a science of protecting information by encoding it into an unreadable format. Cryptography is an effective way of protecting sensitive information as it is stored on media or transmitted through network communication paths. Although the ultimate goal of cryptography, and the mechanisms that make it up, is to hide information from unauthorized individuals, most algorithms can be broken and the information can be revealed if the attacker has enough time, desire, and resources. So a more realistic goal of cryptography is to make obtaining the information too work-intensive to be worth it to the attacker
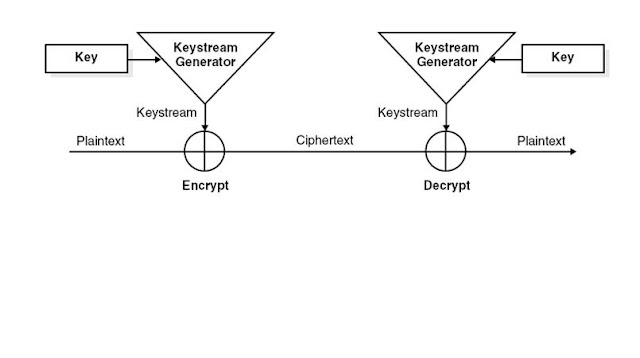
• Encryption is the conversion of data into a form, called cipher text, that cannot be easily understood by unauthorized people. Decryption is the process of converting encrypted data back into its original form , called plaintext so it can be understood.
• In order to easily recover the contents of an encrypted data, the correct decryption key is required. The key is an algorithm that undoes the work of the encryption algorithm (cipher).
Why Cryptogrpahy?
Security is a major concern on the Network, especially when you're using it to send sensitive information between parties.
• Credit-card information
• Social Security numbers
• Private correspondence
• Personal details
• Sensitive company information
• Bank-account information
CIPHER
• A cipher (or cipher) is an algorithm for performing encryption and decryption — a series of well-defined steps that can be followed as a procedure. An alternative term is encipherment. In non-technical usage, a “cipher” is the same thing as a “code”; however, the concepts are distinct in cryptography. When using a cipher the original information is known as plaintext , and the encrypted form as cipher text. The cipher text message contains all the information of the plaintext message, but is not in a format readable by a human or computer without the proper mechanism to decrypt it.
BLOCK CIPHERS
• In cryptography, a block cipher is a symmetric key cipher which operates on fixed-length groups of bits, termed blocks, with an unvarying transformation. When encrypting, a block cipher might take (for example) a 128-bit block of plaintext as input, and output a corresponding 128-bit block of ciphertext. The exact transformation is controlled using a second input — the secret key. Decryption is similar: the decryption algorithm takes, in this example, a 128-bit block of ciphertext together with the secret key, and yields the original 128-bit block of plaintext. DES is a block cipher with a 64 bit block size. AES is a block cipher with a 128 bit block size. RSA and Diffie-Hellman are block ciphers with variable block sizes.
STREAM CIPHERS
• Stream ciphers encrypt plaintext one byte or one bit at a time.Stream ciphers represent a different approach to symmetric encryption from block ciphers. Block ciphers operate on large blocks of digits with a fixed, unvarying transformation.. Stream ciphers typically execute at a higher speed than block ciphers and have lower hardware complexity. However, stream ciphers can be susceptible to serious security problems if used incorrectly: see stream cipher attacks — in particular, the same starting state must never be used twice.
• Example Stream Ciphers A5, the algorithm used to encrypt GSM communications, is a stream cipher. The RC4 cipher and the one time pad are also stream ciphers
• Computers using symmetric-key encryption to send information between each other must have the same key.
• In symmetric-key encryption, each computer has a secret key (code) that it can use to encrypt a packet of information before it is sent over the network to another computer. Symmetric-key requires that you know which computers will be talking to each other so you can install the key on each one. Symmetric-key encryption is essentially the same as a secret code that each of the two computers must know in order to decode the information. The code provides the key to decoding the message.
A substitution cipher is a method of encryption by which units of plaintext are replaced with ciphertext according to a regular system; the "units" may be single letters (the most common), pairs of letters, triplets of letters, mixtures of the above, and so forth. The receiver deciphers the text by performing an inverse substitution.
• Example –
PLAINTEXT abcdefghijklmnopqrstuvwxyz
CIPHERTEXT QRSKOWEIPLTUYACZMNVDHFGXJB
TRANSPOSITION CIPHER
• In a transposition cipher, permutation is used, meaning that letters are scrambled. The key determines the positions that the characters are moved to. This is a simplistic example of a transposition cipher and only shows one way of performing transposition. When introduced with complex mathematical functions, transpositions can become quite sophisticated and difficult to break. Most ciphers used today use long sequences of complicated substitutions and permutations together on messages. The key value is inputted into the algorithm and the result is the sequence of operations (substitutions and permutations) that are performed on the plaintext.
• In cryptography, an S-box is a basic component of symmetric key algorithms which performs substitution. In block ciphers, they are typically used to obscure the relationship between the Key and the ciphertext .
• In general, an S-box takes some number of input bits, m, and transforms them into some number of output bits, n: an m×n S-box can be implemented as a lookup table with 2m words of n bits each. Fixed tables are normally used, as in the Data Encryption Standard (DES), but in some ciphers the tables are generated dynamically from the key; e.g. the Blowfish and the Twofish encryption algorithms.
DATA ENCRYPTION STANDARD
• DES has been implemented in a majority of commercial products using cryptography functionality and in almost all government agencies. It was tested and approved as DES is a block encryption algorithm. When 64-bit blocks of plaintext go in, 64-bit blocks of ciphertext come out. It is also a symmetric algorithm, meaning the same key is used for encryption and decryption. It uses a 64-bit key, 56 bits make up the true key, and 8 bits are used for parity. When the DES algorithm is applied to data, it divides the message into blocks and operates on them one at a time. A block is made up of 64 bits and is divided in half and each character is encrypted one at a time
ASYMMETRIC KEY
• Asymmetric-key encryption, public-key encryption uses two different keys at once -- a combination of a private key and a public key. The private key is known only to your computer, while the public key is given by your computer to any computer that wants to communicate securely with it. To decode an encrypted message, a computer must use the public key, provided by the originating computer, and its own private key. Although a message sent from one computer to another won't be secure since the public key used for encryption is published and available to anyone, anyone who picks it up can't read it without the private key. The key pair is based on prime numbers (numbers that only have divisors of itself and one, such as 2, 3, 5, 7, 11 and so on) of long length. This makes the system extremely secure, because there is essentially an infinite number of prime numbers available, meaning there are nearly infinite possibilities for keys. One very popular public-key encryption program is Pretty Good Privacy (PGP), which allows you to encrypt almost anything.
• RSA. are the initials of the three creators: .Rivest, Shamir, and Adleman. One of the biggest problems in public key cryptography is the distribution of keys. There are many ways of passing the cipher to the other person, but there is risk of getting the key stolen by an unauthorized person. So in order to overcome this problem “Trap-door” ciphers were discovered. The “Trap-door” ciphers work on the one-way methodology, i.e. then anyone in the world can encode a message, but only one person can decode it. For each cipher, there is a key for encoding and a different key for decoding. We have to make up a decoding key Da and generate the corresponding encoding key Ea. The receiving person does exactly the same thing, but he makes up a decoding key Db and generates the corresponding encoding key Eb. You tell him Ea (but not Da) and he tells you Eb (but not Db). Then you can send him messages by encoding using Eb (which only he can decode) and vice-versa . He encodes messages to you using Ea (which only you can decode, since you're the only person with access to Da).
RSA working
• It is very simply to multiply numbers together, especially with computers. But it can be very difficult to factor numbers.
• For example, if we are asked to multiply together 34537 and 99991, it is a simple matter to multiply these numbers and get the product 3453389167. But the reverse problem is much harder.
• RSA encryption works like this. We’ll find two huge prime numbers, p and q that have 100 or maybe 200 digits each. We’ll keep those two numbers secret (they are
private key), and we will multiply them together to make a number N = pq. That number N is basically our public key. It is relatively easy to get N, It just need to multiply two numbers. But if you know N, it is basically impossible for you to find p and q. To get them, you need to factor N, which seems to be an incredibly difficult problem.
• In the following example, suppose that person A wants to make a public key, and that person B wants to use that key to send A a message. In this example, we will suppose that the message A sends to B is just a number. We assume that A and B have agreed on a method to encode text as numbers. Here are the steps:
• 1. Person A selects two prime numbers. We will use p = 23 and q = 41 for this example, but keep in mind that the real numbers person A should use should be much larger.
• 2. Person A multiplies p and q together to get pq = (23)(41) = 943. 943 is the public key., which he tells to person B (and to the rest of the world, if he wishes).
• 3. Person A also chooses another number e which must be relatively prime to (p -1)(q - 1). In this case, (p - 1)(q -1) = (22)(40) = 880, so e = 7 is ne. e is
also part of the public key, so B also is told the value of e.
• 4. Now B knows enough to encode a message to A. Suppose, for this example, that
the message is the number M = 35.
• 5. B calculates the value of C = Me(mod N) = 357(mod 943).
• 6. 357 = 64339296875 and 64339296875(mod 943) = 545. The number 545 is
the encoding that B sends to A.
• 7. Now A wants to decode 545. To do so, he needs to find a number d such that
ed = 1(mod (p -1)(q - 1)), or in this case, such that 7d = 1(mod 880). A solution is d = 503, since 7 * 503 = 3521 = 4(880) + 1 = 1(mod 880).
• 8. To find the decoding, A must calculate Cd(mod N) = 545503(mod 943). This looks like it will be a horrible calculation, and at first it seems like it is, but notice that 503 = 256+128+64+32+16+4+2+1 (this is just the binary expansion of 503). So this means that
545503 = 545256+128+64+32+16+4+2+1 = 545256545128 …… 5451
• But since we only care about the result (mod 943), we can calculate all the partial
results in that modulus, and by repeated squaring of 545, we can get all the exponents that are powers of 2. For example, 5452(mod 943) = 545 545 =297025(mod 943) = 923. Then square again: 5454(mod 943) = (5452)2(mod 943) = 923 923 = 851929(mod 943) = 400, and so on. We obtain the following table:
5451(mod 943) = 545
5452(mod 943) = 923
5454(mod 943) = 400
5458(mod 943) = 633
54516(mod 943) = 857
54532(mod 943) = 795
54564(mod 943) = 215
545128(mod 943) = 18
545256(mod 943) = 324
So the result we want is:
• 545503(mod 943) = 324.18.215.795.857.400.923.545(mod 943) = 35:
• Using this tedious (but simple for a computer) calculation, A can decode B's message and obtain the original message M = 35.











Comments